1、范数满足的三个特性

① 非负性：||x||≥0||x||≥0，且||x||=0||x||=0当且仅当x=0x=0时成立 。

② 齐次性：||k⋅x||=|k|⋅||x||||k⋅x||=|k|⋅||x|| 

③ 三角不等式： ||x+y||≤||x||+||y||

 

2、向量的范数

0-范数，向量中非零元素的个数

1-范数，计算方式为向量所有元素的绝对值之和

 

 

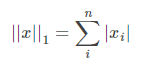
2-范数，计算方式跟欧式距离的方式一致。

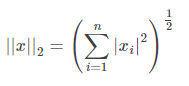
2、矩阵的范数

1-范数，又名列和范数。顾名思义，即矩阵列向量中绝对值之和的最大值。

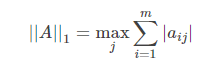
2-范数，又名谱范数，计算方法为A^TA的矩阵的最大特征值的开平方。

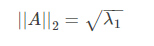
其中λ₁为A^TA的最大特征值。